皆様こんにちは。
AMDlabの翟です。
アイキャッチ画像は、相島で出会った猫の写真です。格好よく撮ろうとしたのですが、なぜかちょっと怖い表情に写ってしまいました(でも、実際にはとても人懐っこくて、撫でさせてもらえました!)
業務の中でよく登場するテーマの一つに「最適化」があります。
しかしながら、「最適化」という言葉が具体的に何を意味するのか、分かりにくいと感じる方も少なくないかもしれません。
そこで今回では以下の三点からわかりやすく整理してご説明したいと思います。
1.最適化とは、単目的最適化と多目的最適化の違い
2.最適化の方法論
3.Grasshopperの最適化プラグイン
内容としては理論的な部分が中心となりますが、最後に実際の応用を紹介したブログ記事のリンクも掲載していますので、併せてご覧いただければ幸いです。
はじめに
「最適化」とは、実は私たちが日常生活の中でも自然に行っている行為です。
旅行や買い物の選択、SNSのレコメンド、地図アプリの経路探索など――複数の条件を天秤にかけて意思決定する、その背後には常に最適化のロジックが働いています。
そして、「なぜその選択をしたのか?」を考えると、費用・時間・快適性・利便性といった要素が影響していることに気づきます。これらを整理して数値化し、変数として扱うことで、計算的に最適な選択を導くことができるのです。
1.単目的最適化と多目的最適化の違い
Grasshopperで最適化を行う際、まず理解しておくべきなのが「単目的最適化」と「多目的最適化」の違いです。
単目的最適化
・単一の評価基準(目的関数)に対して最小値または最大値を求める。
・変数は複数でもよいが、結果は唯一解として収束する。
・例:建物の形状を最適化して日射量を最小化する。
多目的最適化
・複数の評価基準を同時に考慮し、それらの間でバランスを取る。
・一意の解は存在せず、パレート最適解と呼ばれる「トレードオフ解の集合」が得られる。
・例:敷地内に複数棟を配置して採光・通風・眺望・容積率を同時に最適化する。
2. 最適化の方法論
最適化にはいくつかの考え方(Approach)と、それを実現する方法論(Methodology)が存在します。ここでは三つの代表的な考え方と、それに対応する方法論を紹介します。具体的な問題に応じて適切な方法を選び、調整する必要があります。
方式1:逐次的に変数を調整して唯一解を得る(逐次探索 / Iterative Search Approach)
最適解を得る過程で、必要に応じて変数が増減する。データを分析し、さらに変数を追加して検討を重ね、最終的に唯一の解に到達する。すなわち、動的に探索を繰り返して収束するアプローチ。
Approach
変数を一つずつ増やしながら分析を繰り返し、最終的に唯一解に収束させるアプローチ。
・問題の解像度を上げていく。
・一つのルートで掘り下げていく。
・問題の解像度を段階的に上げ、一つのルートを深掘りしていく。
Methodology
・局所探索法(Local Search)
・ヒルクライミング(Hill Climbing)
・焼きなまし法(Simulated Annealing)
例:旅行計画
最初は「費用のみ」で最適化、次に「時間」を追加、さらに「快適性」を追加、最終的にすべてを満たす解に絞り込む。
方式2:多目標を単目標に簡略化する(加重和法(Weighted Sum Method))
Approach
・複数の基準を一つの指標にまとめ、単目的最適化として扱う。
・典型例は「コストパフォーマンス」のような比率指標。
Methodology
・加重和法(Weighted Sum Method)
・効用関数法(Utility Function Method)
例:空調システムの成績係数(COP)
・冷暖房能力の最大化(十分な出力を確保)
・消費電力の最小化(コスト削減・省エネ)
・効率の向上(投入エネルギーに対する有効出力)
・環境負荷低減(CO₂削減、冷媒影響の抑制)
→ これら複数の基準を「出力 ÷ 入力」という1つの指標にまとめて評価します。
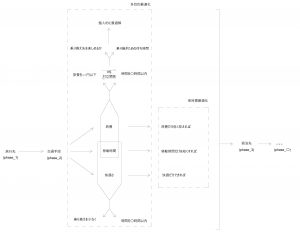
方式3:多段階最適化(動的計画法 / Dynamic Programming)
Approach
・問題を複数のステージに分け、逐次的に意思決定を行う。
・各段階の選択が次の段階に影響し、複数のルートが存在し得る。
・結果的に「意思決定ツリー」のような形になる。
・優先順位、重み付けが存在する。
Methodology
・動的計画法(Dynamic Programming, DP)
・多段階最適化(Multi-stage Optimization)
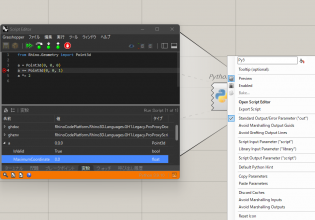
3.Grasshopperの最適化プラグイン
最適化のアルゴリズムは日々進化しており、それに伴って最適化を行うためのツールも数多く存在します。
ここでは個人的に代表になる三つのプラグインを取り上げてご紹介します。
Galapagos(GA/EA)
特徴:
Grasshopper標準搭載の最適化ツール。UIがシンプルで導入が容易。
アルゴリズム:
・Genetic Algorithm(遺伝的アルゴリズム, GA)
・Exploratory Annealing(焼きなまし法, EA)
利点:
・単目的最適化に特化しておりシンプル。
・探索能力が高く、複雑な解空間でも解を見つけやすい。
欠点:
・多目的最適化には対応していない。
・計算コストが高く、収束に時間がかかることが多い。
Wallacei(NSGA-II)
特徴:
多目的最適化を前提とした進化的アルゴリズムプラットフォーム。パレートフロントを可視化できる。
アルゴリズム:
・NSGA-II(非優越ソート遺伝的アルゴリズム)
利点:
・複数の目的を同時に扱え、解のバランスを分析できる。
・世代ごとの進化過程を追跡できる。
・複数解の分布を直感的に理解可能。
・結果の分析に強い。
欠点:
・設定項目が多い
・分析するにはやや手間かかる
Opossum
特徴:
Surrogate Model(代理モデル)を用いた効率的な最適化。特に計算負荷の大きい問題に強い。
アルゴリズム:
・単目的:model‐based RBFOpt、evolutionary CMA‐ES
・多目的:RBFMOpt、NSGA‐II、MACO、MOEA/D, NSPSOなど
利点:
・少ない試行回数で良質な解を得られる。
・計算コストの高い CFD や構造解析と相性が良く、スピードに優れる。
・目標・多目標の両方に応用可能。
欠点:
・近似モデルの精度に依存するため、真の最適解からずれる場合がある。
・初期データの設定が解の品質に大きく影響
おわりに
今回は最適化の理論的な部分について触れてみました。
ブログの中に他に最適化に関する記事が書かれております。
単目的最適化:【Ladybug+Honeybee】×【galapagos】日射解析とグリッドサイズの最適な設定について 応用編
Wallaceiの操作マニュアル:多目的最適化プラグインWallaceiについて~解析編~と多目的最適化プラグインWallacei について~解読編~
Wallaceiで多目的最適化:【Ladybug+Honeybee】×【Wallacei】多目的最適化を実装してみる ルーバー編
Wallaceiで解析と結果の可視化:多目的最適化プラグインwallaceiにつて~出力編~
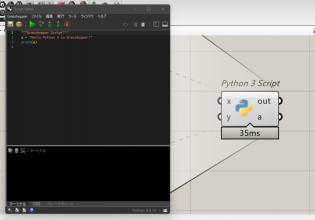
Tunny(もう一つの最適化プラグイン):【Grasshopper】Tunnyを使って最適化をやってみよう!
Octopusの操作マニュアル:多目的最適化プラグインOctopusについて
などの記事をご参考にしていただければ幸いです。
AMDlabでは、開発に力を貸していただけるエンジニアさんを大募集しております。少しでもご興味をお持ちいただけましたら、カジュアルにお話するだけでも大丈夫ですのでお気軽にご連絡ください!
中途求人ページ: https://www.amd-lab.com/recruit-list/mid-career
カジュアル面談がエントリーフォームからできるようになりました。
採用種別を「カジュアル面談(オンライン)」にして必要事項を記載の上送信してください!
エントリーフォーム: https://www.amd-lab.com/entry
AMDlabのSNSアカウントです!ぜひフォローお願いします✨
■ X(旧Twitter):https://x.com/amdlabinc
■ Instagram:https://www.instagram.com/amdlabinc/
■ Facebook:https://www.facebook.com/amdlab.lnc/



COMMENTS