【Grasshopper】ドラゴン曲線を作る Ver.1

皆様こんにちは。
AMDlabの齋藤です。

今回はドラゴン曲線を作ろうと思います。
今回作るものは以下のようなものです。

Dragon curve pic.twitter.com/RqNBtjbKRj

— K. SAITO (@Saito63364078) May 1, 2022

内容としてはあまり難しくありませんが、GHPython-IronPythonから RhinoCommon API を使います。
それでは、始めてみましょう！

今回のデータはこちらに挙げております。
https://github.com/AMDlab/TechBlog-Create_Dragon_curve_v1

ドラゴン曲線とは？

まず、ドラゴン曲線について説明します。Wikipediaによれば

ドラゴン曲線（ドラゴンきょくせん、英語: Dragon curve）とは、L-system（リンデンマイヤー・システム）のような再帰法を用いて構成することの出来る、ある自己相似性フラクタルの族に含まれている曲線のことを言う。

のだそうです。
さらに筑波大学の三谷さんによると

細長い紙を半分、半分、半分、、
と折ってから、それぞれの折り目が90度になるように開くと、ドラゴン曲線が現れるの面白いから、やってみて。

ドラゴン曲線 – Wikipedia https://t.co/2WZgHkPiOf pic.twitter.com/lfn6ZcRuZc

— 三谷純 Jun MITANI (@jmitani) May 1, 2022

こちらで簡単に作ることができるそうです。
ただもっと正確で複雑なドラゴン曲線を作りたく、今回はGrasshopperで作りました。

アルゴリズムについて

WikipediaではL-systemと呼ばれるアルゴリズムで作成していましたが、
今回は折った紙を開くようなアルゴリズムで作っていこうと思います。

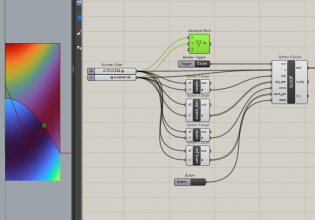
STEP 1: Grasshopperで既存コンポーネントをつなげて作る

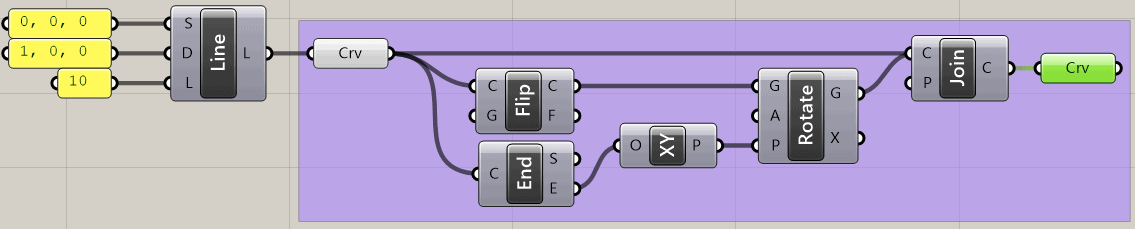
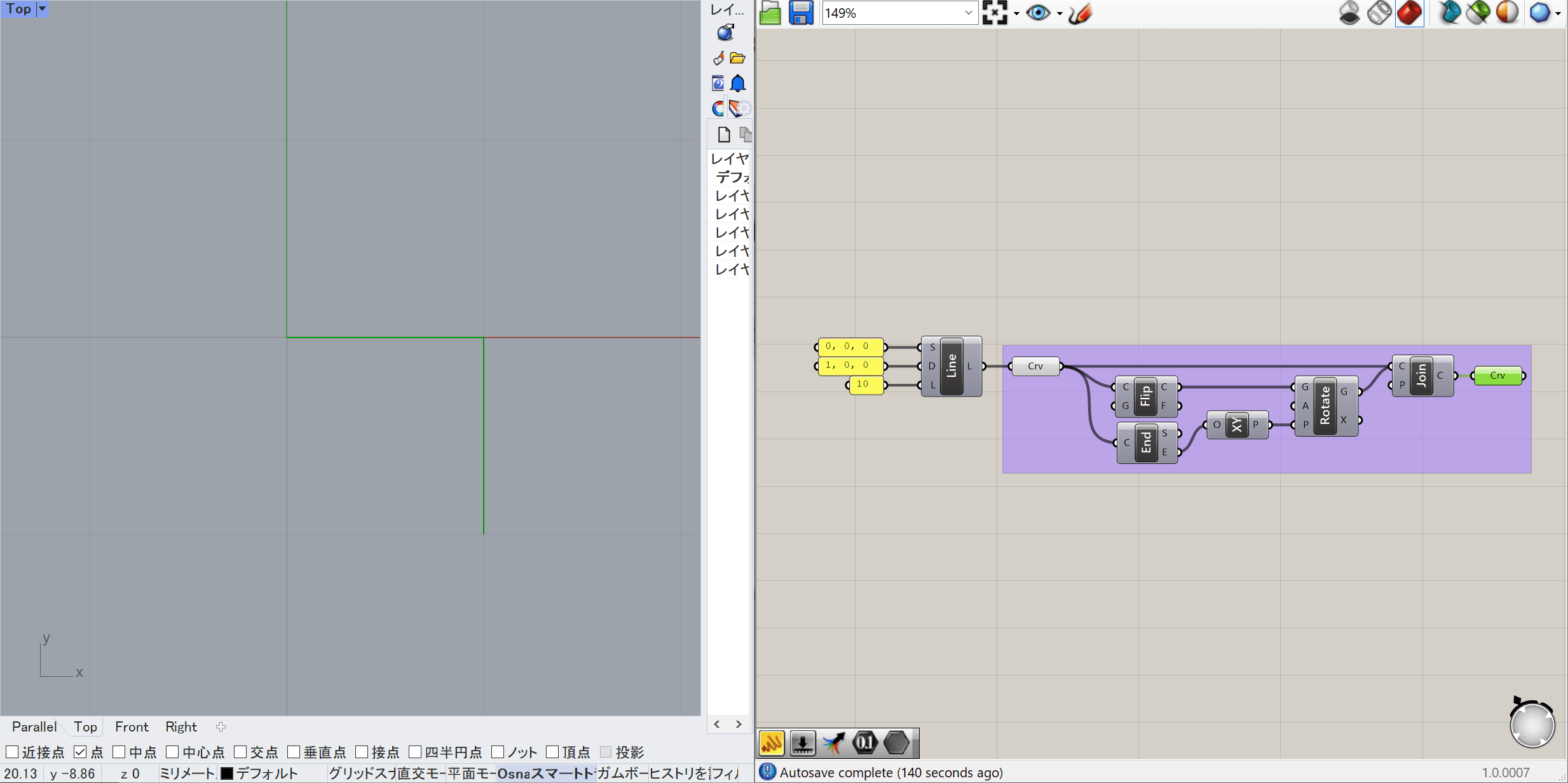
まず今回作るアルゴリズムを理解するために、1度Grasshopperの元々あるコンポーネントをつなげて作ってみましょう。
以下のようにコンポーネントをつなげます。

ドラゴン曲線の既存コンポーネントでの作成(文字)

ドラゴン曲線の既存コンポーネントでの作成(アイコン)

中身は、

LineSDLで初期の線分を作る。
Group内
1. 元の曲線の方向を反転させる。
2. 元の曲線の終端を中心に2.1の曲線を90度回転させる。
3. 元の曲線と2.2の曲線をくっつける。

ようにしています。そうすると、以下のように図ができます。

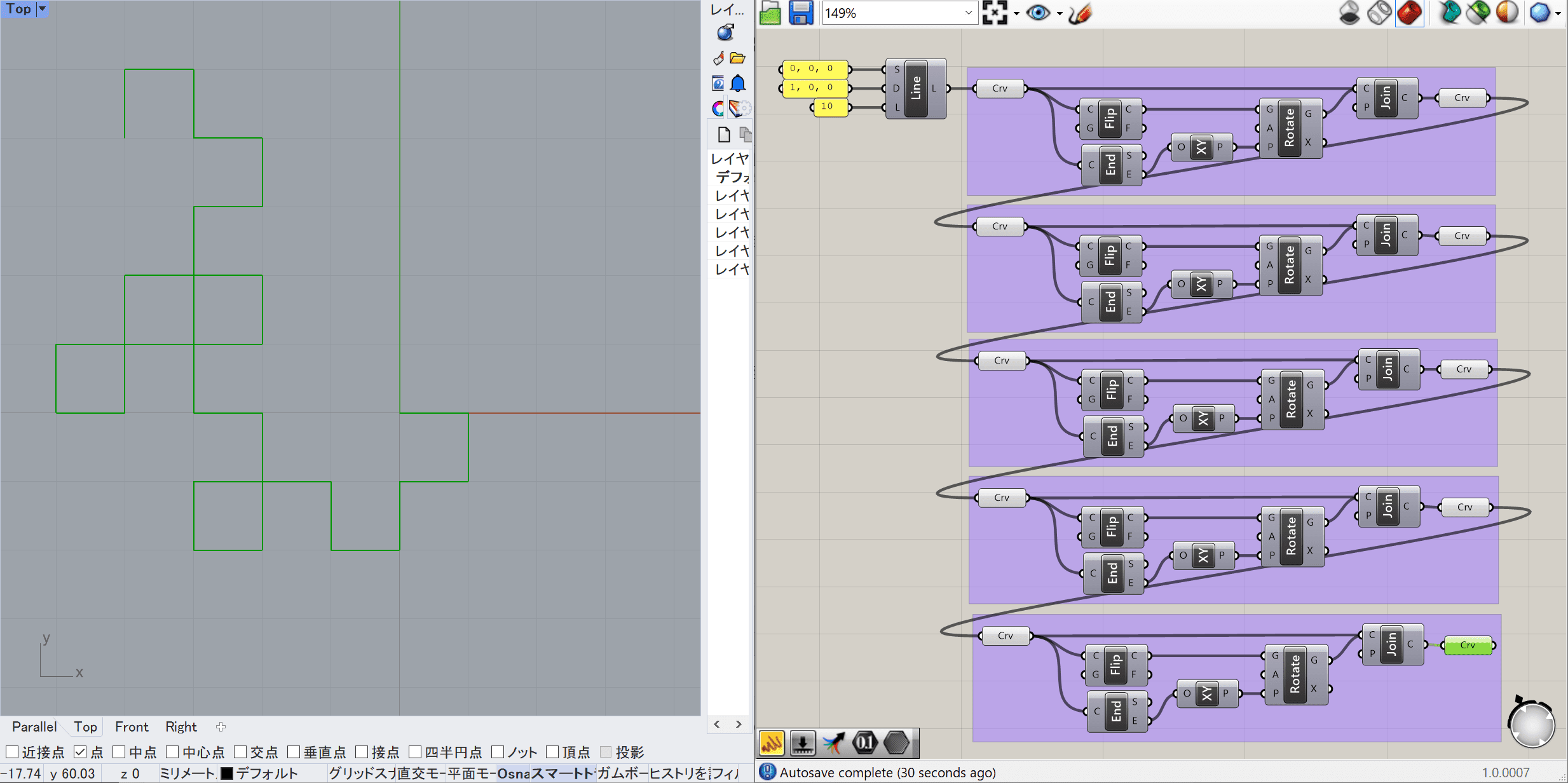
あとはこのGroupを複製してつなげていけば、簡単にドラゴン曲線が出来上がります。

しかし、ドラゴン曲線をより複雑に、次元を深めようとするには、コピペしてつなげるを繰り返さなければならずスマートではありません。
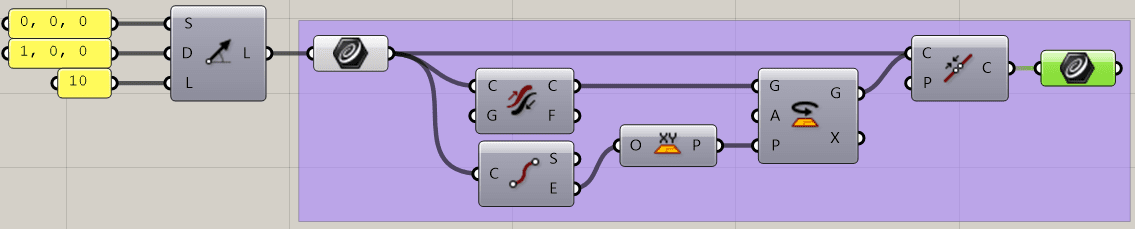
そこで、次はGHPythonで書いてみましょう！

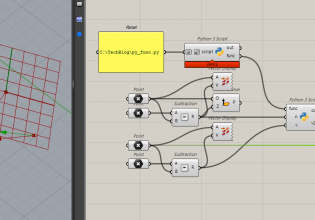
STEP 2: GHPythonからRhinoCommon APIを叩いて作る

次はGHPythonを使って簡単にドラゴン曲線をより複雑に書いてみましょう。
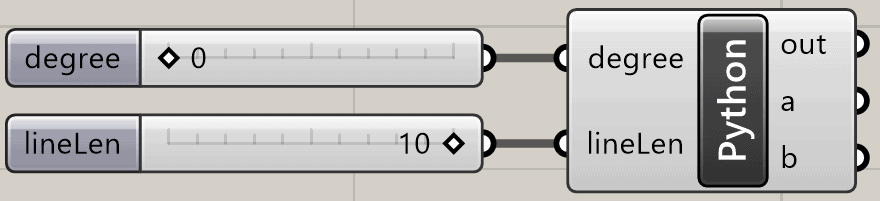
GHPythonはこのように作ります。

ここで、スライダーの degree は、

Slider TypeはIntegers
範囲は0<1440

スライダーの lineLen は、

Slider TypeはIntegers
範囲は0<10

としており、Python側のType hintは、 degree が int 、 lineLen が float となっています。

次にPythonをいじっていきます。
方法はRhinoPythonで使え、デフォルトで出てくる rhinoscriptsyntax やGrasshopperコンポーネントを直で触れる ghpythonlib.components 等ありますが、今回はIronPythonから RhinoCommon API を叩いてみようと思います。

中身はこのようになっています。
STEP 1でやったアルゴリズムと同じようにして、繰り返す部分をfor文で書いている様子です。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

from Rhino.Geometry import *

from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]

pts = Polyline(pts)

for i in range(0, degree-89, 90):

cachePts = pts.Duplicate()

cachePts.Reverse()

cachePts.RemoveAt(0)

tr = Transform.Rotation(

radians(90),

Vector3d(0, 0, 1),

pts.Last)

cachePts.Transform(tr)

pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

ここからはこのプログラムを説明していきます。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

1	from Rhino.Geometry import *

RhinoCommon API の Rhino.Geometry 内の関数をワイルドカードを使ってすべて使えるようにします。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

2	from math import radians

度数法で入力した数値を弧度法( radians )に直す関数を使えるようにします。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

4 5	pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)] pts = Polyline(pts)

pts を初期化します。
Rhino.Geometry 内の Point3d クラスでx=0, y=0, z=0の点とx= lineLen , y=0, z=0の点を pts に入れ、
pts を Rhino.Geometry 内の Polyline クラスに変化させます。

POINT： Polyline クラスでは RhinoList を継承しているため、List関連の Last プロパティや AddRange 関数等が使えます。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

7	for i in range(0, degree-89, 90):

for文でループさせます。
range() の中身はstart=0, end=degree-89, step=90となっています。
つまり、 i の変数が0～ degree -89まで90ずつ増えるようになります。
i は使っておりませんが、詳しく説明すると、
例えば degree が360の場合、 i は0, 90, 180, 270と変化し、
degree が359の場合、 i は0, 90, 180と変化、
degree が1の場合、for文自体実行されません。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

cachePts = pts.Duplicate()

cachePts.Reverse()

cachePts.RemoveAt(0)

tr = Transform.Rotation(

radians(90),

Vector3d(0, 0, 1),

pts.Last)

cachePts.Transform(tr)

pts.AddRange(cachePts)

for文の中身です。内容は、

pts を cachePts へ複製させます。
cachePts を反転させます。
最後に合わせるとき点が被らないよう cachePts の0番目を消します。
変形のクラス Transform を作ります。
ここでは、 Transform.Rotation を使って、90回転させたい, 回転の軸を(0, 0, 1), 回転の中心を pts の最後の点として変形のクラス Transform を作っています。
cachePts を4の変形のクラスで変形させます。
pts に cachePts を拡張します。

このようにしています。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

18	a = pts.ToNurbsCurve()

最後に pts をNurbsCurveにして a に出力します。
これでGHPythonの中身の完成です。
スライダーの degree を増やすことでドラゴン曲線が描けるようになると思います。

これで楽に複雑なドラゴン曲線を描くことができました。

STEP 3: 紙を開くような動きをさせる

このままだと味気ないので、最後に degree を細かく増やすと紙を開くような動きにします。
方法は、STEP 2のPythonプログラムに以下の文を追加するだけです。これで b に開くような動きを追加できます。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

if degree%90 != 0:
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    tr = Transform.Rotation(
        radians(degree%90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    b = cachePts.ToNurbsCurve()

if degree%90 != 0:

cachePts = pts.Duplicate()

cachePts.Reverse()

tr = Transform.Rotation(

radians(degree%90),

Vector3d(0, 0, 1),

pts.Last)

cachePts.Transform(tr)

b = cachePts.ToNurbsCurve()

中身はSTEP 2のfor文の中身とほぼ同じですので、変更点だけを説明していきます。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

if degree%90 != 0:
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    tr = Transform.Rotation(
        radians(degree%90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    b = cachePts.ToNurbsCurve()

20	if degree%90 != 0:

degree を90で割ったあまりが0でないときに実行します。
ドラゴン曲線が確定した a とまだ動いている途中の b が被るため、このようにしています。

from Rhino.Geometry import *
from math import radians

pts = [Point3d(0, 0, 0), Point3d(lineLen, 0, 0)]
pts = Polyline(pts)

for i in range(0, degree-89, 90):
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    cachePts.RemoveAt(0)
    tr = Transform.Rotation(
        radians(90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    pts.AddRange(cachePts)

a = pts.ToNurbsCurve()

if degree%90 != 0:
    cachePts = pts.Duplicate()
    cachePts.Reverse()
    tr = Transform.Rotation(
        radians(degree%90), 
        Vector3d(0, 0, 1), 
        pts.Last)
    cachePts.Transform(tr)
    b = cachePts.ToNurbsCurve()

tr = Transform.Rotation(

radians(degree%90),

Vector3d(0, 0, 1),

pts.Last)

STEP 2では回転角を90度としていましたが、今回は degree を90で割ったあまりで回転させています。
これで展開していくような動きを追加することができました。確認してみましょう！

いかがでしたでしょうか？
おそらく、より複雑でかっこいいドラゴン曲線が描けたと思います。
今回はGHPython-IronPythonから RhinoCommon API を叩く方法で行いましたが、他2つの方法でも行えます。
ただ、 RhinoCommon API を叩くことに慣れていれば、GHC#やC#で新しくコンポーネントを作ることにも慣れやすくなります。
皆さんもぜひ、使ってみましょう。

BIM: Grasshopper

OpenCVとARUcoマーカーを利用した画像マッピング前の記事

Revit2023アップデート内容次の記事

建築を中心として、3Dモデリング、IoT、デジタルファブリケーション、Webなどの様々なテクノロジーに関する記事を提供しています。