皆様こんにちは。
AMDlabの齋藤です。

それでは、このアルゴリズムを作っていきましょう。

STEP 1: Grasshopperで既存コンポーネントをつなげて作る

---

今回も、作るアルゴリズムを理解するために、1度Grasshopperの元々あるコンポーネントをつなげて作ってみましょう。
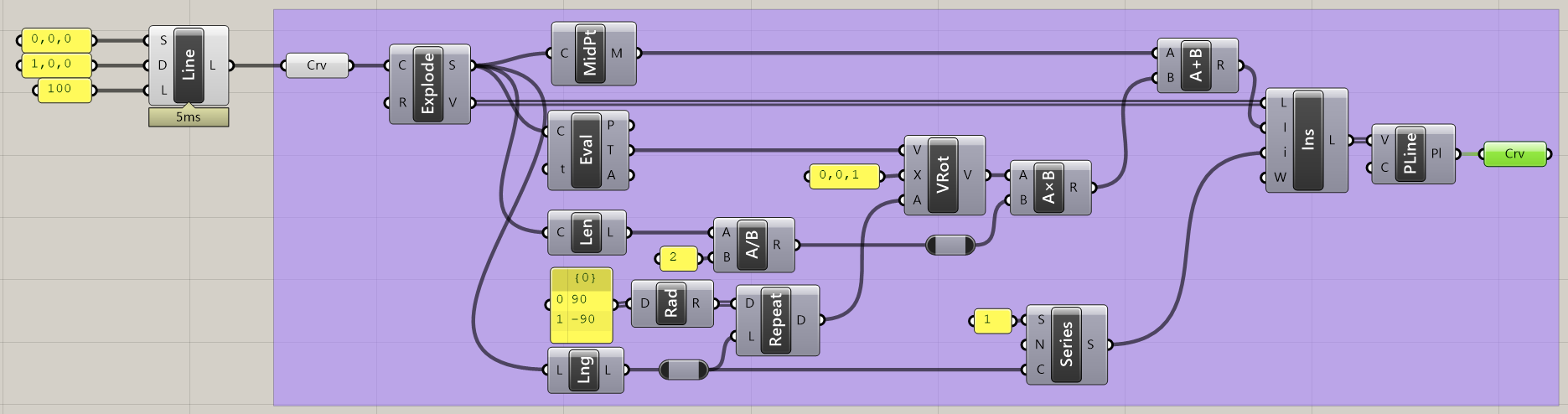
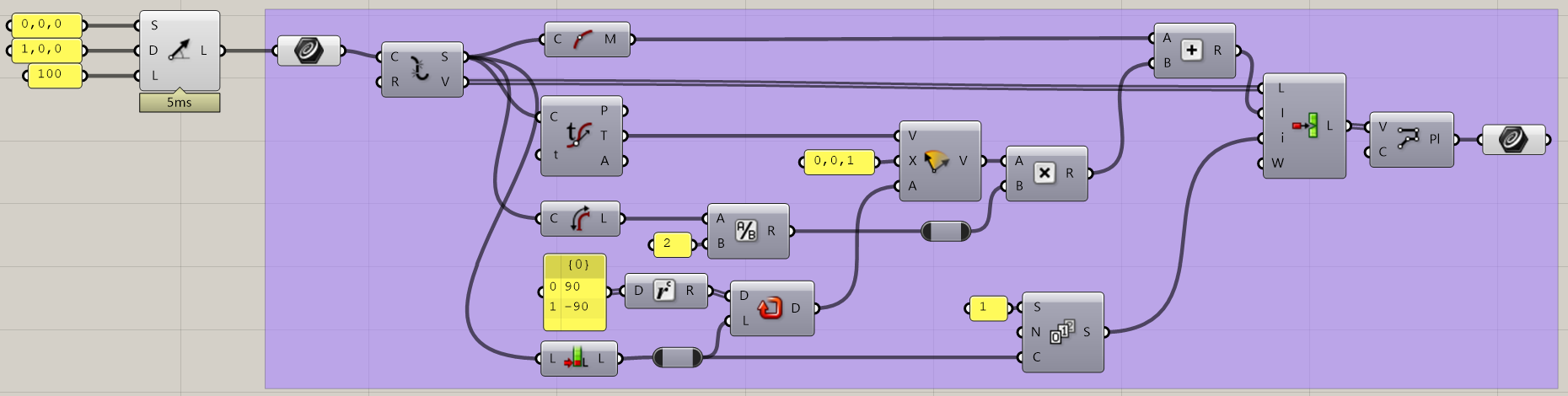
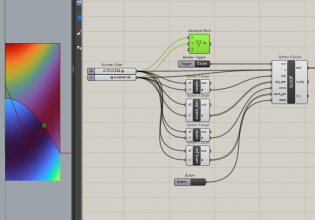
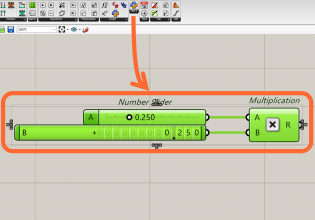
以下のようにコンポーネントをつなげます。

中身は、

1. LineSDLで初期の線分を作る。
2. Group内
   1. まず入力されたPolyline Curveを線分と点に分解します。
   2.  線分から、
      1. 線分の中心を算出し、それを移動する基底とする。
      2. 線分方向を算出する。＆線分の個数から90度方向、-90度方向に移動させるかのリストを繰り返し作成する。
         それらより、移動方向を決定する。
      3. 線分の半分の長さを算出する。
   3. 2.2.1の基点から2.2.2の方向、2.2.3の長さ移動させる。
   4. 分解したPolyline Curveの点の間に2.3で作成した点を入れる。
   5. 点をPolylineにする。

ようにしています。
かなりぐちゃぐちゃに作ってしまったので、作りながらどういうことをしているのか確認しながら作ってみましょう。
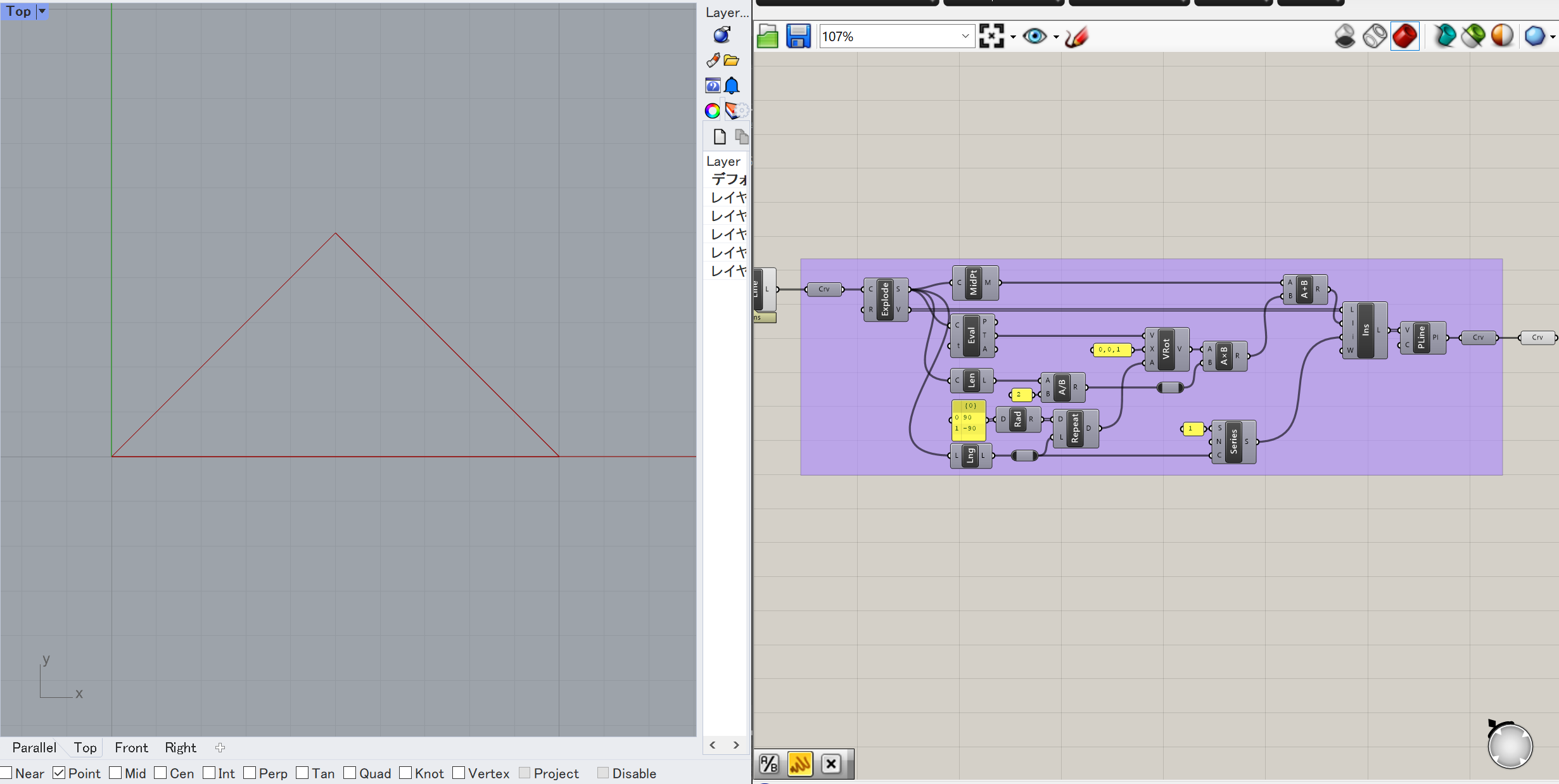
全部できると、以下のように図ができます。

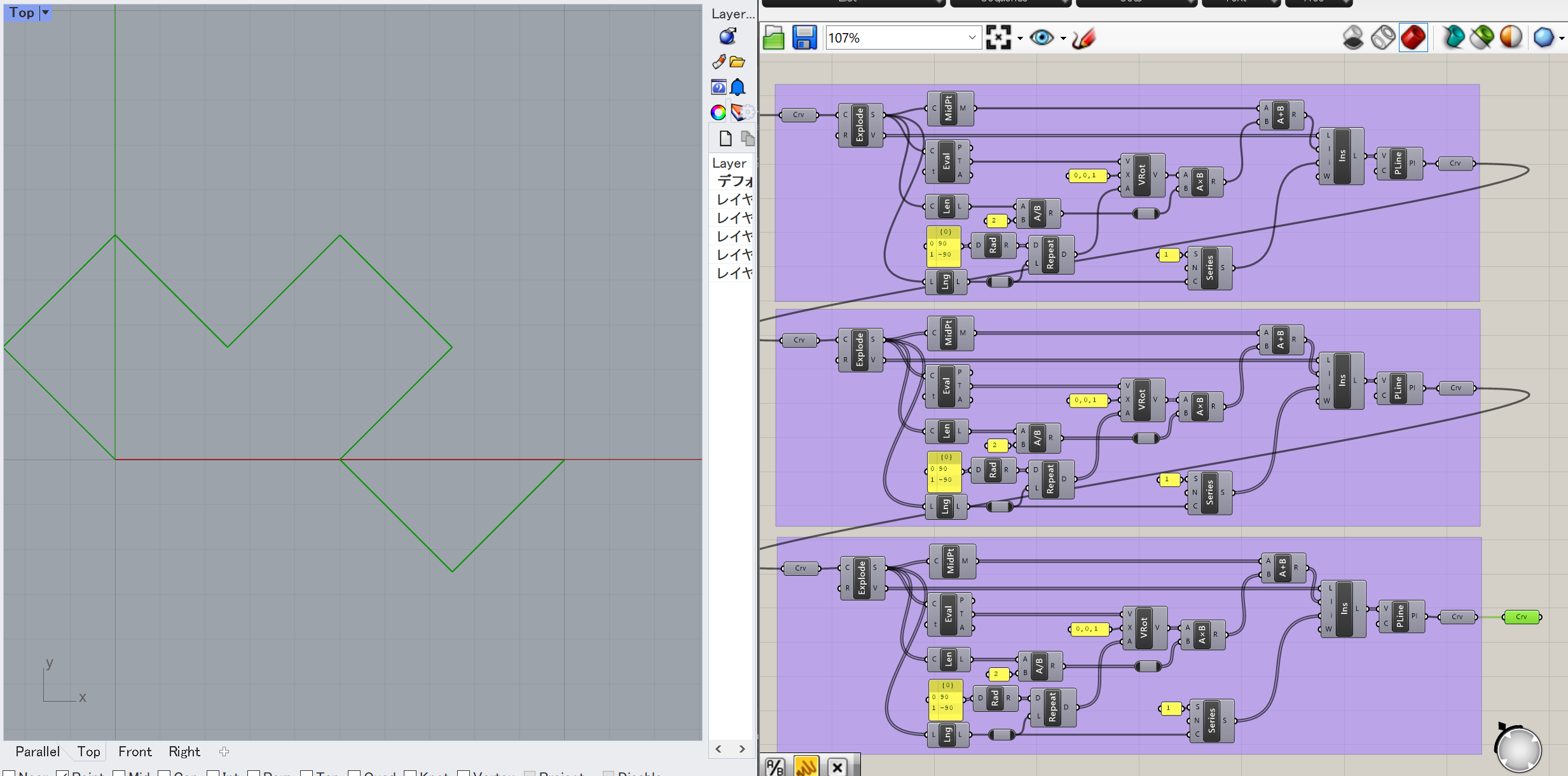
あとはこのGroupを複製してつなげていけば、簡単にドラゴン曲線が出来上がります。

しかし、今回もドラゴン曲線をより複雑に、次元を深めようとするには、コピペしてつなげるを繰り返さなければならずスマートではありません。
そこで、次はGHPythonで書いてみましょう！

STEP 2: GHPythonからRhinoCommon APIを叩いて作る

---

次も前回と同じようにGHPythonを使って簡単にドラゴン曲線をより複雑に書いてみましょう。
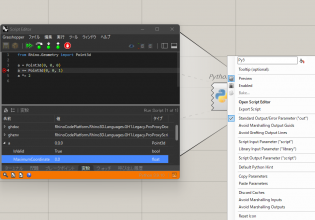
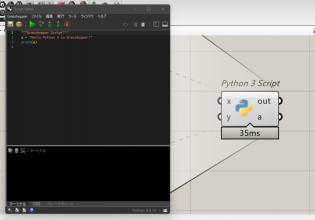
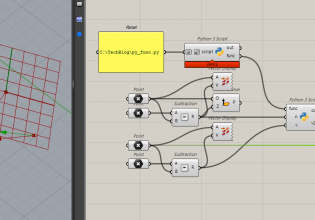
GHPythonはこのように作ります。

ここで、スライダーの foldCount は、折る回数（次数）で、

• Slider TypeはFloating point
• 範囲は0<14

スライダーの lineLen は、初期の線長で、

• Slider TypeはIntegers
• 範囲は0<100

スライダーの widthPerLL は、線幅と1線長の割合(width per line length)で、

• Slider TypeはFloating point
• 範囲は0<1.00

としており、Python側のType hintは、 foldCount が float 、 lineLen が int 、 widthPerLL が float となっています。

次にPythonをいじっていきます。
今回もIronPythonから RhinoCommon API を叩いてみようと思います。

中身はこのようになっています。
STEP 1でやったアルゴリズムとほぼ同じようにしていますが、2.4の”分解したPolyline Curveの点の間に2.3で作成した点を入れる。”(Insert Items)については、少し違った方法で入力しています。

ここからはこのプログラムを説明していきます。

 

RhinoCommon API の Rhino.Geometry 内の関数の Point3d, Polyline を使えるようにします。
前回はワイルドカードを使って簡単に使えるようにしましたが、本来はこちらのように使うものだけ指定して使うのがワイルドカードでの関数被りもなくなり、丁寧です。
切り捨ての関数( floor )と平方根の関数( sqrt )も使えるようにしておきましょう。

 

次に入力された変数から実際に使う変数を作ります。
fCInt は foldCount を切り捨てた数を入れます。これが折れた回数となります。
dLen は折れた後の線分の長さを示しています。
w は線幅を計算しています。

POINT：線幅と折れた後の線分の長さとの比を統一することで、図が荒い場合は太く、図が細かい場合は細くすることができます。

 

pts を初期化します。
使えるようにした Point3d クラスでx=0, y=0, z=0の点とx= lineLen , y=0, z=0の点を pts に入れます。

 

flag に True を入れておきます。

 

fCInt 回(折れた回数、次数分)for文を回します。

 

pts listに沿ってfor文を回します。

POINT： pts listはfor文の中でlistの要素数が増えるため、 range(start, end, step) で逆方向に要素を選択して、それらの対応をしなくていいようにします。

例)　[0, 2, 4, 6]の配列に[1, 3, 5]を互い違いに入れようとするとindexを順方向で入れようとすると、
[0, 2, 4, 6]         -> [0, 1, 2, 4, 6]　　　　　 この時のindexは1
[0, 1, 2, 4, 6]     -> [0, 1, 2, 3, 4, 6]　　　　 この時のindexは3
[0, 1, 2, 3, 4, 6] -> [0, 1, 2, 3, 4, 5, 6]　　　  この時のindexは5
となりますが、(今回は1,3,5になってくれる配列なので、そのアルゴリズムを作ってもいいのですが)

indexを逆方向で入れようとすると、
[0, 2, 4, 6]         -> [0, 2, 4, 5, 6]　　　　　 この時のindexは3
[0, 2, 4, 5, 6]     -> [0, 2, 3, 4, 5, 6]　　　　 この時のindexは2
[0, 2, 3, 4, 5, 6] -> [0, 1, 2, 3, 4, 5, 6]　　　  この時のindexは1
このように-1ずつするだけでinsertさせることができます。

 

for文の中身です。内容は、

1. 中点( cp )を算出する。
2. 直線の方向と長さ( v )を算出する。
3. flagNum を作成する。
4. cp と v のXY反転したものを加算し newP に入力する。
5. pts の j+1 番目に newP を入れる。
6. flag を逆にする。

ここでいくつかPOINTがあります。

POINT： flag をfor文を回すごとに反転することで右、左、右、左、…といったようにさせられる。

POINT：(for文内容の3-4) flag を数字として扱い、 True の場合 flagNum が +1 、 False の場合 flagNum が -1 となるようにする。
元々Python上では、 True を1、 False を0として扱うことができます。これを利用して、
flag-0.5 で、 True の場合 0.5 、 False の場合 -0.5 となり、それの2倍で True の場合 +1 、 False の場合 -1 となるようにしています。
このようにして、 flagが True の場合に右へ、 flag が False の場合に左へ行くプログラムを作ります。

 

最後に pts を Polyline 、 NurbsCurve にして a に出力します。

これでGHPythonの中身の完成です。
スライダーの foldCount を増やすことでドラゴン曲線が描けるようになると思います。

これで今回も楽に複雑なドラゴン曲線を描くことができました。

STEP 3: 移動途中の動きをつくる

---

このままだと味気ないので、最後に foldCount を細かく増やすと少しずつ折れてくるように、
移動途中の動きを作っていきます。

方法は、STEP 2のPythonプログラム 18-20行の間に以下の文を追加するだけです

中身はSTEP 2のfor文の中身とほぼ同じですので、変更点だけを説明していきます。

 

d に foldCount の小数点以下を入力します。 foldCount が2.45の場合、 d は0.45のような感じです。

 

先ほど計算した d で v を加算する度合を調整します。
これで移動途中の動きを作れました。確認してみましょう！