【Grasshopper】Craneで折り紙シミュレーション

皆様こんにちは。
AMDlabの齋藤です。
少し前にInkjet 4D Print[1]が話題に上がりました。
ざっと説明をすると、シートに印刷してそのあとにお湯等で熱を与えると狙った形に自動変形するというものです。
こんな感じで私も折り紙を自動変形させたいなと感じています。

今回はこちらでよく設計に使われるCrane[2]を使って、waterbomb pattern(なまこ折りとも呼ばれる)の折り紙シミュレーションをしたいと思います。

今回のデータはこちらに挙げております。
https://github.com/AMDlab/TechBlog-Crane-Waterbomb-Pattern

インストール

インストールはfood4rhinoからPackageManegerでできます。
food4rhino：https://www.food4rhino.com/en/app/crane
今回は現時点での最新バージョンである0.2.4を使用していきます。
インストールできると以下のコンポーネントが表示されます。

CMeshを作る

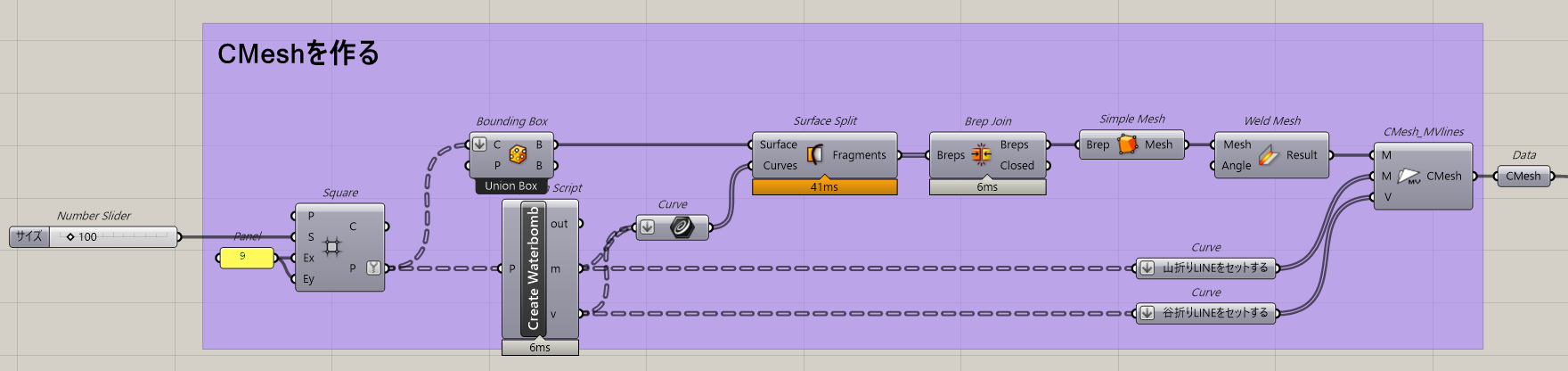
CMesh_MVlinesからCMeshを作ります。
CMesh_MVlinesではMeshと山折り、谷折りのLineを入力することでCMeshを作成します。
そのため、山折り、谷折りの線とそれらを使ったMeshを作成します。

まず、元となるグリッドをSquareで作成します。
入力のSizeのみスライダー入力とします。

次に山折り、谷折りの線を引きます。
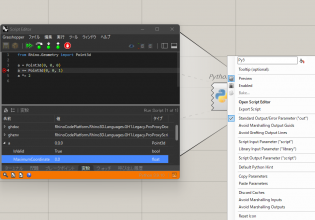
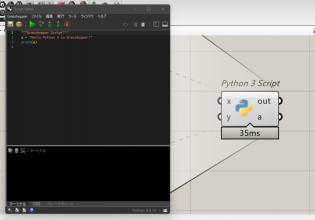
この線はGHPythonで引いていきます。以下がその例です。

説明していきます。

ここではimportをしています。
TreeをListに直す＆戻す関数とLineクラスを呼んでいます。

ここではTreeをlist in listに直しています。
ラムダ式を入れることで、どのようなTreeでもラムダ式で指定する形式に落とし込むことができます。
ラムダ式の説明は他サイトにお任せしますが、
lambda x: x[0] がデフォルトで、今回使用しているものは lambda x:x で、主にSimplifyされたTreeに対して有効です。

リストを変数に入れます。ここで line_m は山折りの、 line_v は谷折りのlist in listになります。

ここで谷折り(山折り)となる線を入力します。
pythonの range 関数を使って i や j を動かします。
range 関数は range(stop_int) の場合、0から stop_int まで動きます。
range(start_int, stop_int, step_int) の場合、 start_int から stop_int まで step_int 分飛び飛びで動きます。
例として range(0, 10, 2) の場合、0, 2, 4, 6, 8と動きます。
後はLineに始点と終点を渡して線を引いていきます。

ここでlist in listをTreeに直しています。
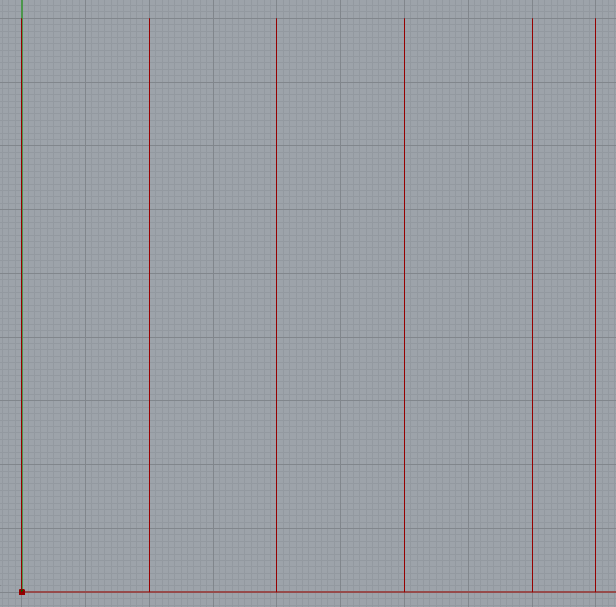
これで出力できる形になりました。上記のみを実行させると以下のようになります。

あとは上記の9-14行を複製していき、 range 関数の中身を適度に調節すれば山折り、谷折りの線ができます。
適度に調節したものは以下より閲覧できます。
https://github.com/AMDlab/TechBlog-Crane-Waterbomb-Pattern/blob/main/create_waterbomb.py

次にCMeshを作るMeshを作成します。

グリッドからBounding Box-Union Boxでグリッド全部を内包するBounding Box(Flat Box)を作成し、
上記で作成した山折り、谷折りの線でSplitさせます。
そのあと、JoinでくっつけてMesh化し、Weld MeshでWeld状態にします。

あとはCMesh_MVlinesに上記で作成したMeshと山折り、谷折りを入れればCMeshの完成です。
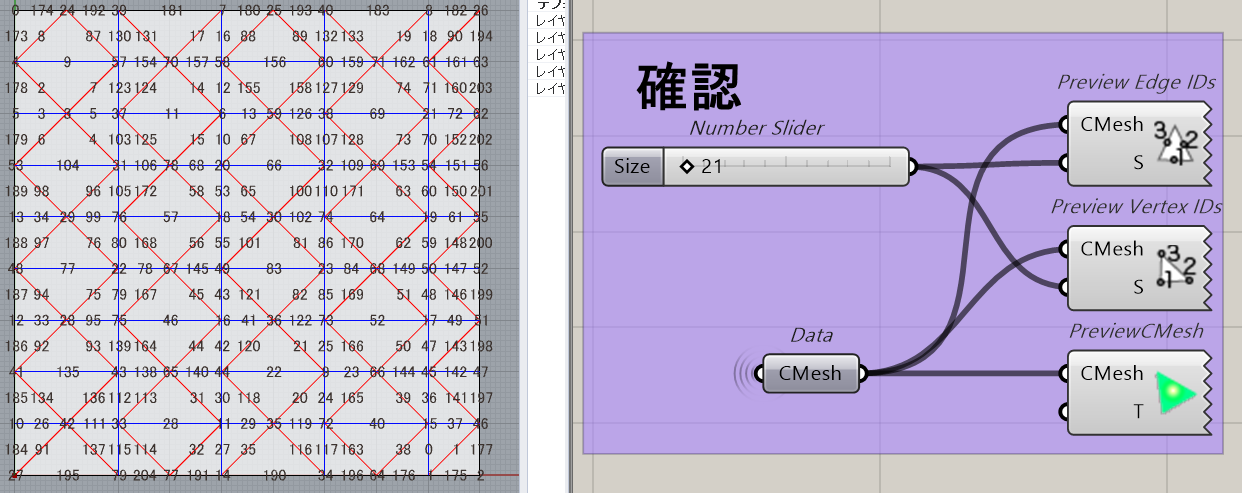
以下でしっかり作成できているか確認をしてみます。

青線が谷、赤線が山になっています。しっかりできていそうです！

折り紙シミュレーションを動かす

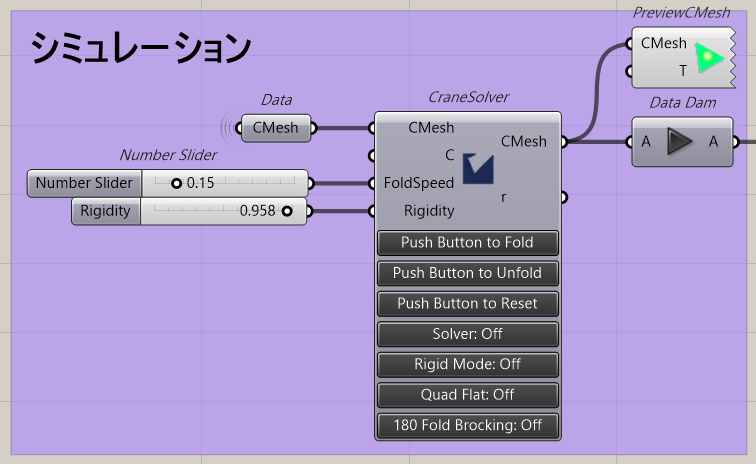
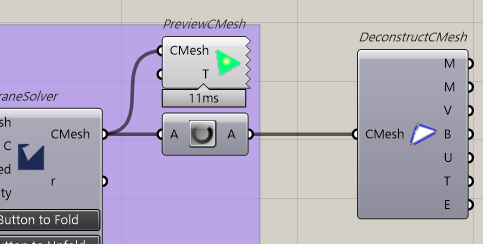
次はCraneSolverを使って折り紙シミュレーション動かします。

CraneSolver先ほど作ったCMeshを入れます。そして折る速度と剛性の度合をFoldSpeed、Rigidityとして入力します。
これでシミュレーションができます。あとは見やすいように出力からPreviewCMeshへCMeshを表示させれば完了です。
実際に動かしてみましょう。
Rigid ModeとSolverをOnにしてPush Button to Foldを押せば折り始めます。

しっかり折れました！Push Button to Resetを押すと元の入力に戻ります。

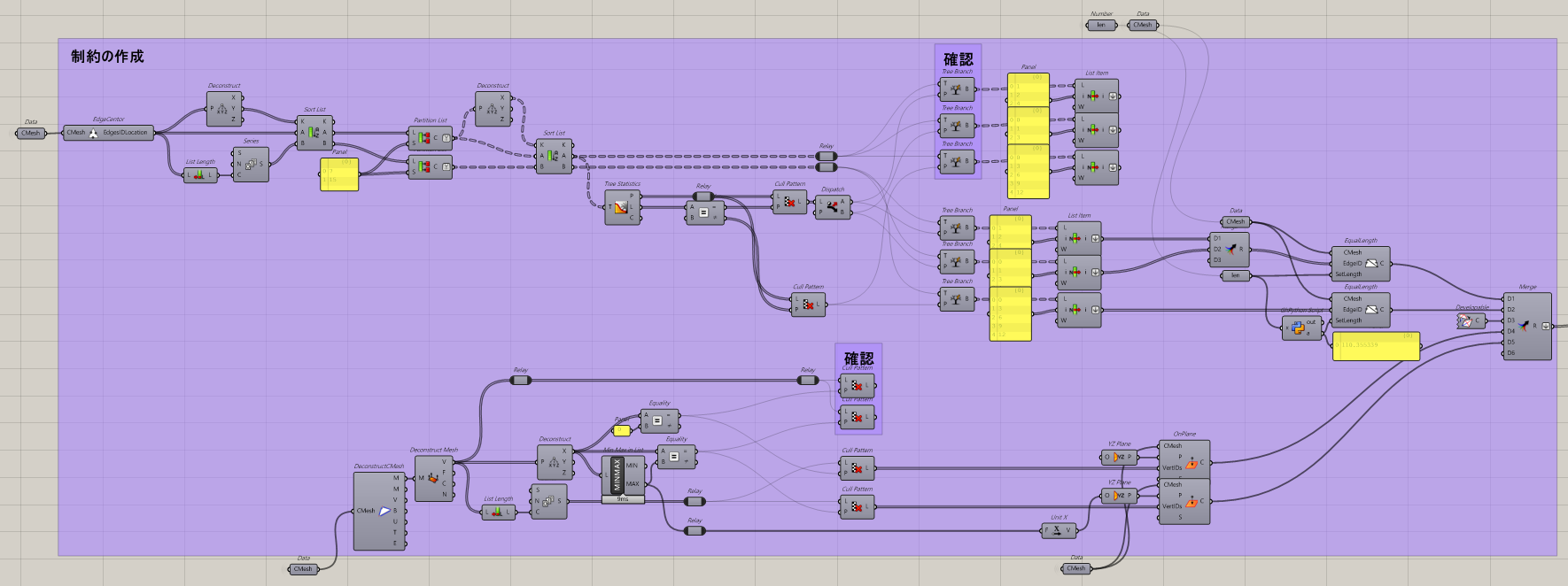
制約を設ける

最後に制約を設けて面白い形状を生成したいと思います。
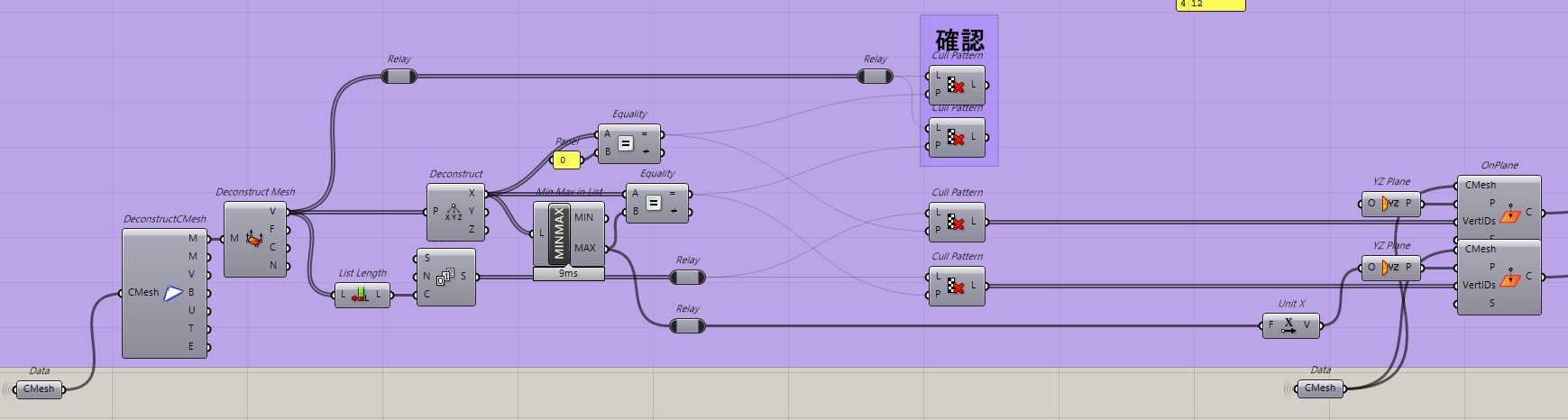
今回は辺の長さ、展開可能、点をある平面上に置く制約をEqualLength、Developable、OnPlaneで実装していきます。

まずは辺の長さの制約です。
EqualLengthの実装はCMeshと辺の番号そして指定する長さを入力することで指定する辺の長さへ変形させます。
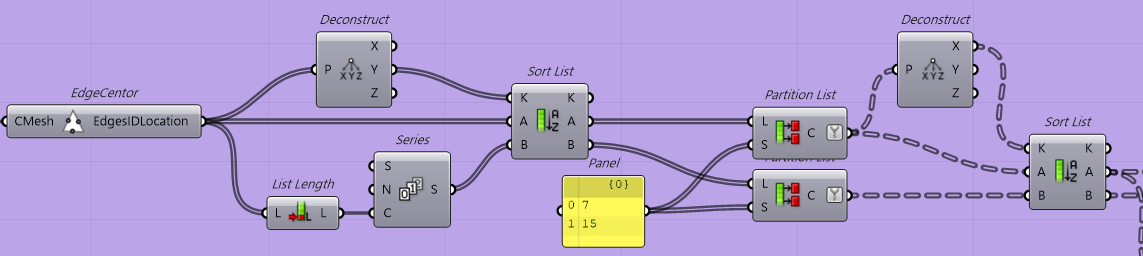
しかし、辺の番号がわからないためSort Listで番号を辺の中心位置でソートしていきます。

これでソートができました。
Sort Listの出力のAが辺の中心位置でBが辺の番号です。
あとは指定する位置の辺番号と辺の長さを指定してあげればよいです。

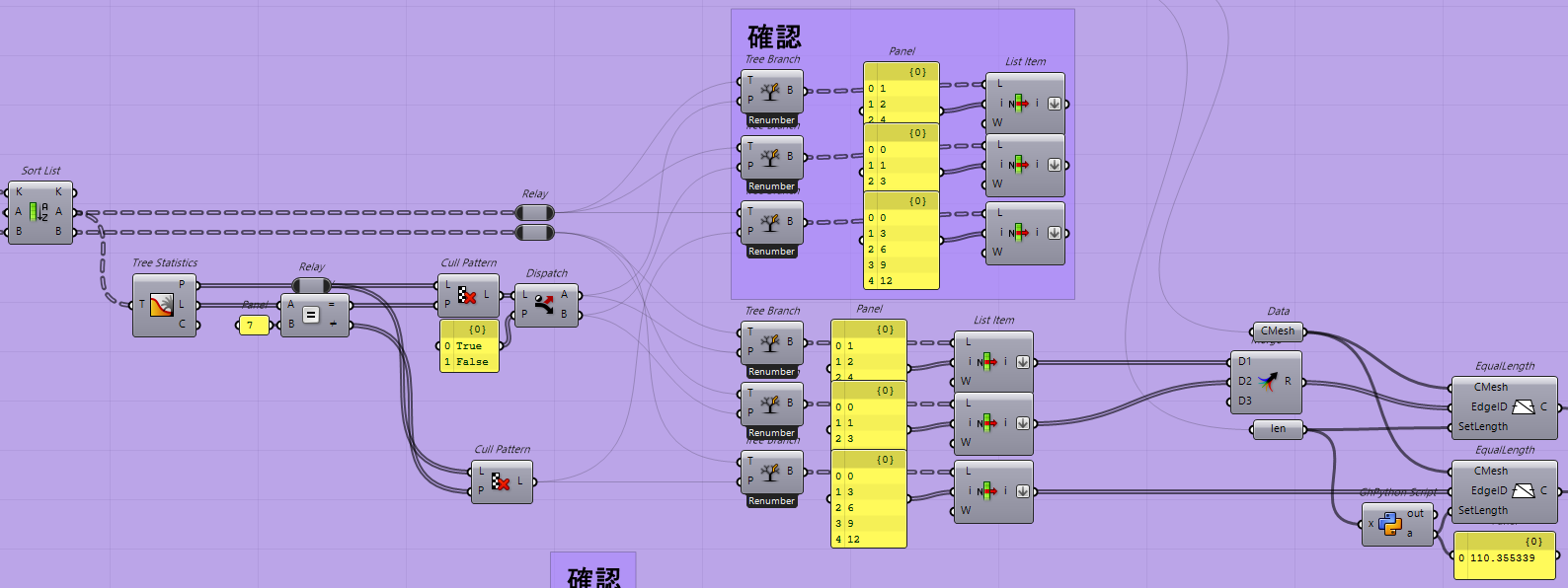
確認のグループで今回指定する辺の中心位置が確認できます。
さらに右下で行っているGHPythonは以下になります。

これで辺の長さの指定ができました。

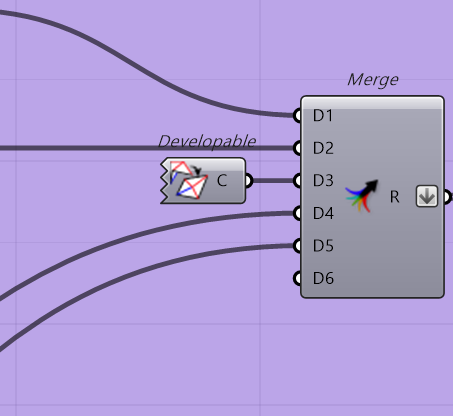
次に展開可能にする制約ですが、以下のコンポーネントでできます。

最後に点を平面上に置く制約です。
OnPlaneの実装はCMeshと点の番号そして平面を入力することでできます。
しかしこちらも、点の番号がわからないためそれらを見つけなければなりません。
そこで今回はモデルの左右にある点（Ｘが0である点、最大となる点）に対してYZ平面上に入れようと思います。

こちらも確認グループで今回指定する点が確認できます。
これで点を平面上に置く制約ができました。

これで全ての制約が作成できました。
制約を適用してみます。適用方法は CraneSolverのCに入力することで適用されます。
適用させたら実際に動かしてみます。今回はRigid Modeはoffのまま動かしてみます。

パラメーターを動かすと辺が変形できました。
次もRigid Modeはoffのまま折ってみます。この状態で折ると制約条件上のまま、制約条件に乗っていない辺等が変化、変形しながら折られます。

無事折れることができました。

シミュレーションを動かすときの注意点です。
このあと出てきたデータを利用してKangarooで展開させましたが、CraneSolverをその後に動かすと、こちらの操作を受け付けないようになってしまいました。
ですので、PreviewCMesh以外に繋ぐ場合はData Damを挟むことをお勧めします。
Kangarooで展開方法は時間があればまた記事にしたいと思います。

おわりに

今回のシミュレーションでやったものを紙に印刷し、実際に折ってみました。

展開までできれば実際に折ることもできるので、皆さんもぜひやってみてください！

参考文献

[1] Koya Narumi, Kazuki Koyama, Kai Suto, Yuta Noma, Hiroki Sato, Tomohiro Tachi, Masaaki Sugimoto, Takeo Igarashi, and Yoshihiro Kawahara.2023. Inkjet 4D Print: Self-folding Tessellated Origami Objects by Inkjet UV Printing. ACM Trans. Graph. 42, 4 (August 2023), 13 pages. https://doi.org/10.1145/3592409
[2] Crane. https://www.food4rhino.com/en/app/crane. Kai Suto, Kotaro Tanimichi

BIM
Grasshopper
Tech
python
ARTICLES