はじめまして!AMDlabの柴田と申します!
今回はpythonを使ってアルゴリズムの基本を学ぶために、Big O Notation(Big O 記法)について触れていこうと思います。
そもそもアルゴリズムとは?
問題を解決するための手順や計算方法
・プログラミングを作成する基礎
・システムパフォーマンス向上
・システムの保守性の向上
上記の様に定義づけることができますが、エンジニアがコードを書く上でただ動くコードからパフォーマンスを考慮するとなるとアルゴリズムの理解が必要になってくるかと思います。データ量、ユーザー数が多いアプリケーションは自ずと数秒でも早いコードが求められるケースが発生するかと思いますので、今回はアルゴリズムを学ぶ最初のステップとしてご参考にして頂けたらと思います。
まず、アルゴリズムの性能はどのように評価すればよいのでしょうか?アルゴリズムは、かかった時間で評価することは困難です。なぜなら、同じアルゴリズムで記述されたプログラムでも、実行環境やハードの性能が違えば、まるで違った結果になってしまうからです。
そのため、アルゴリズムの性能を評価するために計算量という指標が用いられます。
この場合においての計算量とは処理時間がどれだけ掛かるのかを示しているのですが、「10秒かかった」などの時間を用いるのではなく、「命令数」を基準とします。
計算量の記述にはO記法(オーダーきほう)という表記が用いられるのが一般的になります。この「O」はオーダー(Order)という単語に由来し、ランダウの記号などとも呼ばれ、実行されるアルゴリズムが、どれほどの時間、記憶領域を使用するかを評価する基準として用いられます。
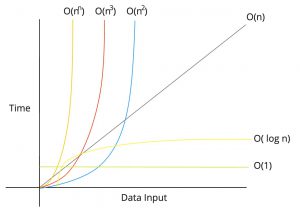
Big O Notation(Big O 記法)
上記は代表的なオーダーの一覧ですが、処理時間の評価としては下記の順番になります。
O(1) < O(log n) < O(n) < O(n log n) < O(n2)
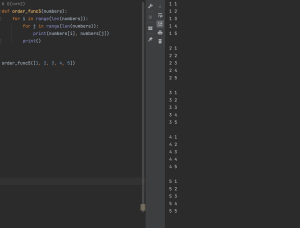
具体的なコードをpythonで記載します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
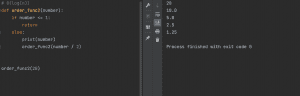
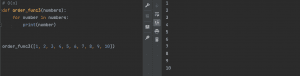
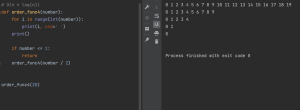
#O(1) def order_func1(numbers): return numbers[0] # O(log(n)) def order_func2(number): if number <= 1: return else: print(number) order_func2(number / 2) order_func2(20) # O(n) def order_func3(numbers): for number in numbers: print(number) order_func3([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) # O(n * log(n)) def order_func4(number): for i in range(int(number)): print(i, end=' ') print() if number <= 1: return order_func4(number / 2) order_func4(20) # O(n**2) def order_func5(numbers): for i in range(len(numbers)): for j in range(len(numbers)): print(numbers[i], numbers[j]) print() order_func5([1, 2, 3, 4, 5]) |
オーダーごとに説明を加えていくと
O(1)
この場合、配列の添字アクセスで定数を取得しているため、計算量としては最も少ないオーダーになります。
O(log n)
データを分割して計算を行うオーダーになります。上記の例では20を2分割しているため、printが4回実行されています。二分木検索などのようにデータ全体を分割しながら行うリニアサーチが例になります。
ちなみにリニアサーチとは配列の中身を一つ一つ確かめていく、最も基本的な探索法になります。
O(n)
こちらは実行例で表示しているように与える引数Nの数によって計算量が変わってくるため、分割して計算を行うO(log n)よりも計算量が多くなります。
O(n log n)
O(log n)と同様にデータを分割するのですが、分割後、それぞれの値に対して計算を行うため、その分計算量が増えるオーダーになります。二分木のオーダー(log n) × リニアサーチのオーダー(n)を掛け合わせた手法です。
O(n2)
次数によって処理数が変わってくるのですが、例のように2の次数の場合、引数をNを2乗した計算にするため、引数Nと次数によって計算量が大幅に変わってきます。
このようにオーダーを知っていると処理時間にある程度の予測を立てる事ができます。パフォーマンスの向上のため、コードを書く一つの指標として、参考にしていただけたと思います。
以上Big O 記法についての紹介でしたが、次回以降私の番では、こちらを基本としてソート、サーチなどのアルゴリズムをご紹介できたらと思います!
参考資料
現役シリコンバレーエンジニアが教えるアルゴリズム・データ構造・コーディングテスト入門
https://www.udemy.com/course/python-algo/
Understanding Big-O Notation With JavaScript
https://betterprogramming.pub/understanding-big-o-notation-c3245b8112dc
アルゴリズムと計算量
http://sevendays-study.com/algorithm/ex-day1.html





COMMENTS